ベクトルの内積R・n は、|R||n|cos(a) と書くことができます。ベクトルn は、unit normal vector (単位放線ベクトル) ですから、|R||n|cos(a) = rcos(a) になります。また、"a" は、2つのベクトルがなす角度ですから、x が Source point 近傍では、下図に示す様に、a=90度になります。つまり、R・n=0 という結果になります。
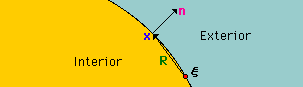
しかし、上の説明では、limR・n=0 or constant as x→ξ になるかどうかの説明になっていませんので、ここでは、x=(x,y) が要素上を移動できる様に、下式で表すことにします。独立変数のηは、Gauss-Legendre 積分の座標です。
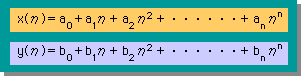
ここに、n は要素の次数です。例えば、n=2 は、2次要素ということになります。
| 先へ進む前に、ここで行いたい事をもう一度、整理しておきます。それは、”要素上の座標 x が、Source point ξ に近づくときに、関数 F(x,ξ) の積分がスムーズに行えるか”です。そのためには、関数 F(x,ξ) の極限(x goes to ξ.) でなく、 F(x,ξ) ds の極限を調べる必要があります。したがって、 F(x,ξ) ds を無次元のGauss-Legendre 積分の座標で表さなくてはなりません。 |
関数 F(x,ξ) をGauss-Legendre 積分の座標系で表した場合は、次の様に書くことができました。詳細については、2次要素を参考にして下さい。
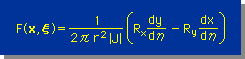
| BACK | NEXT |
|---|
| Menu | Laplace Equation | Taking Limits | Navier's Equation |