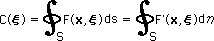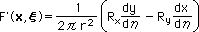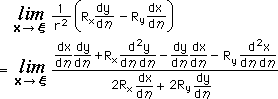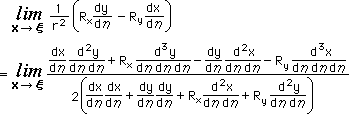Treatment of Free term Integrals
Laplace Equation-4
積分要素の ds を、Gauss-Legendre 積分の座標系へ変換すると、ds=|J|dη になります。よって、関数 F(x,ξ) をC(ξ)の計算式へ代入すると(左下の図)、積分される関数 F'(x,ξ) は、右下の図の様になります。つまり、F(x,ξ) の |J| と ds=|J|dη の |J| がキャンセルアウトされます。
これで、積分要素の ds が持つ次元も関数 F'(x,ξ) へ統合されたことになります。つまり、 F'(x,ξ) の極限を調べれば、C(ξ) のSource point 近傍の特性が分かることになります。
■ lim(R・n)/r2 as x→ξ ■
極限を調べる前に行うことが有ります。それは、関数 F'(x,ξ) のxをξ で置き換えることです。つまり、r=0 とします。実際、やってみると、F'(x,ξ)は、0/0 になってしまします。この様な場合の極限を知るのに威力を発揮するのが、 L'Hospital's rule (ロペタル) です。早速、使ってみましょう。すると、 lim(R・n)/r2 as x→ξ は、次の様になります。
再び、xをξ で置き換えてみます。結果は、分母がゼロになってしまいます。そこで、もう一度、L'Hospital's rule (ロペタル) を使うと、次の結果が得られます。
参考までに、L'Hospital's rule は、何回でも使えます。
