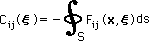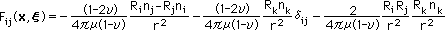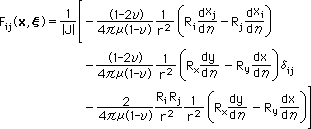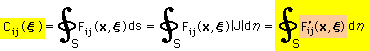Treatment of Free term Integrals
Navier Equation-2
Cij(x,ξ) は、次の式で計算出来ます。
ここで、ちょっと、境界要素法により弾性解析の歴史に触れておきます。境界要素法の弾性解析は、1960年代にKupradze, V. D. (1963, Potential Methods in Theory of Elasticity, Davey, New York) が最初に行ったとされています。有限要素法が発展しはじめてのが、1903年(Fredholm) とされていますので、境界要素法の弾性解析は、60年も遅れて出発したことになります。
■Fij(x,ξ) の展開■
Laplace の F(x,ξ) と違い、Navier の Fij(x,ξ) は、かなり複雑ですので、下に示す様に、項に分解することにします。
続いて、関数 Fij(x,ξ) を無次元のGauss-Legendre積分法の座標で表します。下の様になります。
上の関数を積分すると、Cij(ξ) が計算されることになります。このとき、積分要素のdsも無次元のGauss積分の座標で表す必要があります。つまり、ds=|J|dη です。下図をみて下さい。
