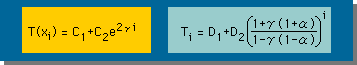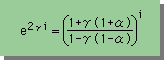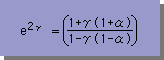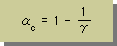
ここで疑問になるのが、αの値です。まず、αの最小値はゼロです。では、最大値はなんでしょう。A=0 と置くと、下式に示す様な値が得られます。

これを Critical α と言います。つまり、使ってはいけないα値です。風上差分では、A=1 (γ=∞) になるようにαを定めています。つまり、α=1 である。ここでは、αの最大値として風上差分を尊重することにしましょう。

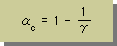
すると、使えるαの値は、次の範囲でCritical αでなければ、どんな数値でも良いことになります。

αの範囲がわかったので、今度はαを決める手だてが必要になってきます。

そこで、提案されたのが、『微分方程式のGeneral solution と 差分式のGeneral solution の値が節点で同じになるように、αを調整してはどうか』というアイデアでした。つまり、数値計算の結果と厳密解を節点で一致させようというのです。

では早速、上のアイデアに基づいて、αの値を計算してみましょう。まず、微分方程式のGeneral solution の中のxは、等分割された要素の長さ(L)で書き表わすと、x=Li になります。そして、ux/k = uLi/k = 2γi になります。i は整数です。

すると、2γi とαを使って、もう一度、微分方程式のGeneral solution と 差分式のGeneral solution を書き下ろすと、次の様になります。

ここで、両者を観察します。両者が同じになるには、次の条件を満足しなくてはなりません。

つまり、次の式を満たすαを求めればよいことになります。

ちょっと面倒ですが、計算を進めると上式をαについて書くことができます。結果は、次の様になります。貴方もトライしてみて下さい。