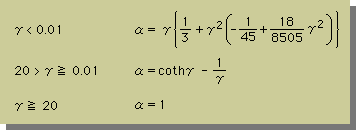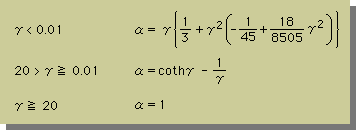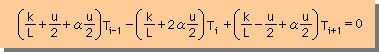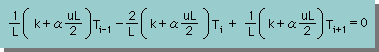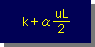ここに、cothγ＝(e^γ+e^-γ)/(e^γ-e^-γ) です。 計算機に組み込まれている関数で cothγを計算すると、γの値によっては、 正しい値を返さないときがあります。 理由は、cothがexpで構成されているからである。そこで、γの値によって次に示す式で計算します。

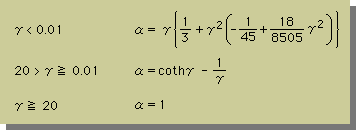上式に示す様に、γが0.01より小さい場合のαの式は、少々複雑になっています。しかし、 γ/3でも解析の精度におおきな影響を与えることはありません。また、αの計算には、 倍精度を使って下さい。

先ほどの、計算例を今度はαを用いて計算してみましょう。グラフで示しても違いが判別できないので、数値を表示することにしました。ここUpwind solution をクリックしてみて下さい。見てわかるとおり、厳密解(Exact)とUpwind solution がまったく同じになっています。この計算に用いたプログラムUPWIND.FORは、ここをクリックするとブラウザーに表示されます。

■αγを加算する意味■
計算が一応成功したところで、 αγをAに加算する意味について考えてみましょう。ここで確認のために、もう一度、AとBを表示します。

上のAとBを、差分式に代入し、k/L を両辺にかけると、次の様になります。

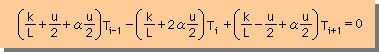この状態から、convective term (u・dT/dx) を取り除くと、微分方程式 kd²T/dxdx =0 を離散化した差分式になるはずである。結果は、次の様になります。

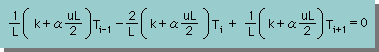式を見ると、k の代わりに下式が熱伝導係数として使われていることになります。

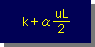この様に、k にαuL/2 を加算することにより、convective-diffusion heat equation で、近似解と厳密解が一致することになります。または、αuL/2 がk に加算されることにより、安定した数値解析が得られることになります。

このαuL/2 を数値解析の分野では、added viscosity とか numerical viscosity とか言います。