■Range of Validity■
地下水の流れは、水頭(後程詳しく説明する)によって記述されています。さらに、Darcyによると、specific discharge は、水頭の空間微分(Hydraulic gradient)に比例しています。つまり、地下水の流れは、線形微分システムで書き表されています。逆にいうと、線形微分システムを保持するためには、幾つかの条件を満たしている必要があります。その、代表例が Reynolds number(Re) です。地下水では、Reynolds number を次の様に定義しています。
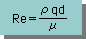
ここに、q=specific discharge, d=平均砂粒の直径です。
Referencesの書物等によると、Re<1 to 10 の範囲で、Darcy's law が有効であるとしています。しかし、地下で起きていることを厳密に把握することは、困難です。さらに、specific Discharge が水頭の空間微分のn乗に比例(つまり、非線形システム)していることが判明してとしても、非線形システムを数値計算することは、適切な判断とはいえません。とりあえず、線形で計算し、予測に使えるかいなかをチェックする方が賢い解決方法といえます。
■Piezometric head (水頭)(h)■
水頭は、hydraulic head、hydraulic potential、Piezometric head等と呼ばれています。意味は、aquifer を流れる水のpotential energy のことです。水のpotential energy とは、下図に示す様に、ある位置(datum line)からenergyを測定したい点までの高さ(重力加速度の180度方向に測定する)に測定点のpressure head (p/γ)を加えた値です。または、potential energy は、測定点の水をhの高さまで押し上げる能力があることを意味しています。 よって、水頭 (h) は、右下に示す式の様に書けます。
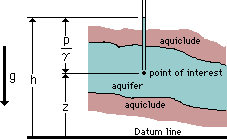 |
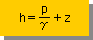 |
上の式は、支配方程式を導く上で、何の役にも立ちませんが、境界条件を設定する上で有効です。
■Transmissivity(T) & Storage coefficient(S)■
河川沿いの堤防やアースダム等を除けば、aquifer の厚さは、水平距離に比べ非常に小さいことが多い。更に、地下水の流れは非常にゆっくりしているため、深さ方向にPitot tube の位置を変えても、hydraulic head の値は大きく変化しないことが知られています。
そこで、実用的な地下水の流れ解析を行うために、Hydraulic conductivity と Specific Storativity の代わりに、下に示すTransmissivity(T) & Storage coefficient(S) がしばしば使われます。
| T=BK | S=BSs |
B は、aquifer の厚さを表します。
以上が、Groundwater を学ぶ時、最初に遭遇する事柄です。これらを理解していないと、支配方程式、境界条件、Dupuit assumption、Well hydraulic、Image well theory、Solute transport、Land Subsidence等の勉強に支障をきたすことになります。
| BACK | NEXT |
|---|
| Menu | Intro | G-EQ3D | G-EQ2D | WELL | Solute |