したがって、水頭を用いると Darcy's Law (つまり、Specific discharge) は、次の様に書けます。
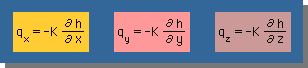
そして、aquifer が isotropic でない場合を考慮すると、Specific discharge は、index notetion でまとめると、次の様になります。
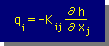
■Hydraulic conductivity(K)■
Darcy's LawのHydraulic conductivityを様々なマテリアルについて実測すると、次の様な結果が得られます。下表の値は、あくまでも目安ですので注意して下さい。
| 固体のタイプ | Hydraulic conductivity in cm/sec |
|---|---|
| 砂利 | 0.1-1.0 |
| 混合砂 | 0.001-0.10 |
| 細砂 | 0.001-0.05 |
| シルトまじりの砂 | 0.0001-0.002 |
| 粘土 | 0.0-0.000001 |
きちんとしたHydraulic conductivityの値については、文献を参考にして下さい。
Hydraulic conductivityについて、もうちょっと物理的意味について考えてみましょう。地下水の流れではありませんが、縦に平行な2枚の板の狭い間(幅=b)を流れる水を考えます(Hele-Shaw model という)。流れは、Laminer になります。すると流体の運動方程式から平均流速は、次の様になります。

上の式を Darcy's law と比較すると、K=(b2/12)(γ/μ) に相当します。つまり、Kは、流体が流れる流路形状パラメーターと流体の特性に分離されています。Aquifer では、b の様にはっきりした寸法は存在しません。よって、Hydraulic conductivityは、下式の様に表すことが出来ます。
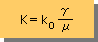
ここに、k0は、[L2]の単位をもっています。γ=単位体積当たりの水の重量(specific weight of water)、 μ=水の粘性係数係数です。
| BACK | NEXT |
|---|
| Menu | Intro | G-EQ3D | G-EQ2D | WELL | Solute |