すると、Transmissivity は、T=K(h-b) と成りますから、支配方程式は、次の様になります。時間項には、S_y の項以外に、S_sh も有ることに注意してください。しかし、S_sは、S_yに比べ非常に小さいため、S_sh も小さいだろうという考えで、S_sh の項は下式がらオミットしてあります。

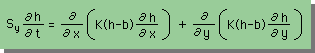
特殊ケースとして、aquiclude(不浸透層)の上面と Datum Line が同じ場合を考えてみましょう。aquicludeの上面の位置を表す変数(b)が常にゼロであるから、支配方程式は、次の様になります。

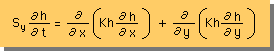
上の2式を、よーく観察すると、式は非線形であることに気付くと思います。このままでは、数値解析に余分な労力を費やさなくてはなりません。そこで、上式のKhのhに平均値を使うと、式は線形になります。つまり、下式の様になります。

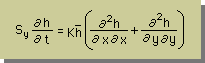
ここでの、例題の紹介はありませんが、前の例題で使ったIMP4Q.FORで解析が行えますので、トライしてみて下さい。

また、上の非線形の式に生成項(N)を追加し、1次元定常の下式にすると、厳密解を得ることが出来ます。暇なときに、厳密解を導いてみて下さい。

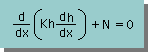
以上が、Groundwaterの水の流れに関する支配方程式です。Groundwaterの本を見ると、まだまだ様々な式が出てきますが、ほぼここで紹介した式に集約することが出来ます。だた1つだけ紹介していない形の式が有ります。それは、Flow to a well です。支配方程式を極座標で書き、well(井戸)に集まる水の量を計算できます。更に、領域のTとSの平均値を、実験的に求めることが出来ます。その他、aquifer の特徴を把握することが出来ます。

しかし、Flow to a well は、FEM解析と深いつながりがないので、ここでは、概要のみの紹介におさえておきます。