Phreatic surface の定常解を求めるためには、下に示す手順が必要になってきます。
| Phreatic surface と Seppage face の位置を仮定して領域を要素分割する。 |
| 境界条件に従って、下のLaplace equation を解く。 |
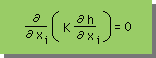 |
| Phreatic surface のノード点において、hydraulic head(h) と z-座標値(z)の値を比較する。 |
| h と z 値が著しく違えば、Phreatic surface のノード点のz-値をhで置き換え、Laplace equation を解く。 |
| h=zであれば、計算終了です。 |
上の手順は、全てソフト上で行う必要があります。したがって、一番やっかいな作業が要素分割です。つまり、ノード点の座標値の変更作業です。場合によっては、下流側のseepage face 付近の要素が、かなり歪になります。
以下に紹介する例題は、プログラムMOVING4BC.FORで計算しています。また、グラフィック作成用の補助ソフトは、MVG4FILE.FOR です。
■x-z 座標 Unconfined Flow の例題その1■
では、早速、計算してみましょう。例題その1として、次の様なaquiferを取り上げてみました。
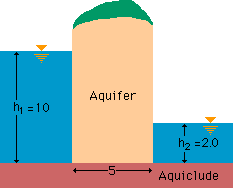
入力データには、FEM4Q.FORで紹介した量に、次の項目が追加されます。下の変数名は、プログラムMOVING4BC.FORで使われています。
| 変数名 | 説明 |
|---|---|
| MAXIT | 繰り返し計算の回数の最大数 |
| ERALLOW | 繰り返し計算を終了できる許容誤差。誤差=最大差/最大値 |
| JPOWER | 座標を移動させるためのパラメーター。後程説明 |
| NGROUP | 座標移動節点のグループの数 |
| NMOVE(I) | 各グループでの節点数 |
| MOVEND(I,J) | 座標移動に関する節点番号。 |
移動節点について、もう少し詳しく述べておきます。節点の座標値を変えても、領域(aquifer)の形を変えては、意味がありません。そこで、移動できる節点をgroupに分けます。i番目のgroupには、NMOVE(I)の節点があります。
| BACK | NEXT |
|---|
| Menu | Intro | G-EQ3D | G-EQ2D | WELL | Solute |