下図にPhreatic surface が上昇しているところを示します。つまり、Phreatic surface は、t=tの位置から、t=t+Δtの位置に移動しています。この時、t=tの面上では、qが外向きに存在しています。すると、Phreatic surface は、qiniΔt/Syの高さまで上昇します。
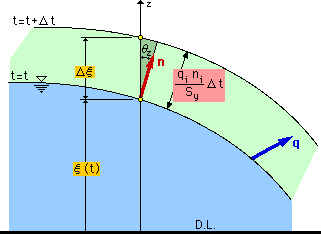
この上昇量は、Phreatic surface に対して垂直方向ですから、水位の上昇(Δξ)は、この高さにcosθzを乗じた値になります。また、Unit normal vector は、
| n=cosθxi+cosθyj+cosθzk |
ですから、cosθzは、nzで表すことが出来ます(下図左)。したがって、これまでの説明を微分方程式で表すと、次の様になります(下図右)。

Phreatic surface の計算で、最も意味のある状態は、定常解です。
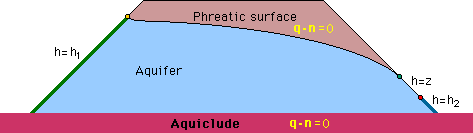
ここでは、計算例として、Phreatic surface の定常解の計算方法を紹介します。下に、計算に必要な境界条件を示します。
| BACK | NEXT |
|---|
| Menu | Intro | G-EQ3D | G-EQ2D | WELL | Solute |