■ プログラムNSEQ8DDSTD.FOR■
ここでは、くさび効果による圧力の計算方法を紹介します。前に紹介した運動方程式から、時間項を取り除き、領域をconfinedとすると、潤滑の支配方程式は、次の様になります。
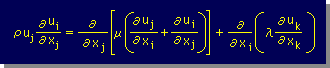
領域をconfined(自由面をもたない)にすると、重力加速度(g)による影響がなくなるため、psとBiの項は、キャンセルされます。念のために、convective terms は、そのままにしておきます。
上式は、xyの2次元です。 座標軸のyは、油膜の厚み方向を示します。一般に潤滑の式は、2次元で油膜の面を表しています。油膜の厚み方向は、連続の式を適用し、油膜の厚さを計算しています。ここでは、連続の式と第2粘性係数を勉強するために、上の式を解くことにします。
プログラムNSEQ8DDSTD.FORは、NSEQ8DD.FORをベースに作成しました。つまり、時間項の1/ΔtをRELAXに替え、定常が出来るだけ短時間で得られるように改造しました。付け加えた変数やsubroutineは有りませんが、新しいΔt計算するSubroutine TIMESTPをSTEPに改めRELAXを計算しています。
Driven cavity flow のところでは、NSEQ8DD.FORを速度分布が定常になるまで計算しましたが、NSEQ8DDSTD.FORを用いても同じ結果が得られるはずです。Reynolds数が1000でも計算できます。 SET4NSSTDNEW.FORでReynolds数1000の計算ができます。使ってみて下さい。 Reynolds数によってRELAXがゼロに到達する場合、有る数値で永遠に続く場合、有る数値で計算が乱れ始める場合の3つの収束が現れます。NSEQ8DDSTD.FORではこれらの3ケースを対処できるようになっています。
■計算例■
では早速、計算してみましょう。計算に使う領域と境界条件は、下図に示す通りです。NSEQ8DDSTD.FORへの入力データは、SETNSLUBNEW.FORで作成しました。
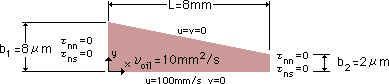
領域は、x軸方向に200要素、y軸方向に10要素で分割しました。要素分割については、また後程ふれます。 粘性係数は、ν=μ/ρ=10mm2/s とし、第2粘性係数は、λ/ρ=1x106xμから1x109xμを選びました。
| BACK | NEXT |
|---|
| Menu | Govern | FEM | 2nd Visco | DCF | Cylinder | /Heat | Lub |