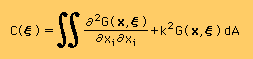
ここで、注意しておいたい事があります。再三、言っていることですが C(ξ) は、ξの位置によって値が違います。そして、境界積分式を解くためには、ξの位置が境界上になくてはなりません。また、解析精度を維持するためには、 C(ξ) をKernel function から求めることが望ましい。つまり、下式で C(ξ) を計算するということです。

しかし、上の式を境界積分に変換することは、多分、不可能ですし、また、領域積分すると境界要素法のメリットがなくなります。そこで、上の式の積分される内容が−δ(x,ξ) であることを利用すると、Laplace equation の C(ξ) が使えることになります。つまり、下式です。

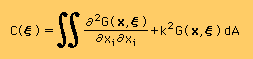
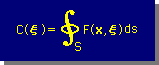
■無限領域でのC(ξ)の計算方法■

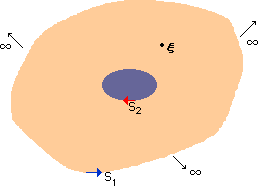左に簡単な無限領域を示します。領域の中に構造物があります。境界要素法でこの領域を計算する場合、この構造物は、hole になります。 左の図で、S1は無限境界上の閉ループ線を意味します。反時計方向になっています。しかし、構造物の境界上のS2は、時計方向になっています。この点に注意して、次のページに進んで下さい。