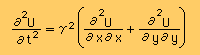
■Wave equation■
Helmholtz Equation について話しを進める前に、元の式であるwave equation について簡単に説明しておきます。
下式は、2次元のwave equation です。変数Uは、(x,y,t)の関数です。
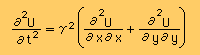
| case | γの意味 |
|---|---|
| 水面波の場合 | 波の速度 |
| 膜の振動の場合 | sqrt(張力/膜の密度) |
| 電磁気学の場合 | 光の速度の関数 |
Wave equation をそのまま直接的に離散化し、数値解析する例は少ないです。 では、どの様に解く例が多いかについて説明します。
数学でおなじみの変数分離(separation of variables) をwave equation に適応すると 変数ごとに Helmholtz equation が導き出されます。 また、wave equation の時間項を hamonic だと仮定すると、同様にHelmholtz equation が導き出されます。 つまり、変数(U(x,y,t))を次の様に書ける場合です。| U(x,y,t)=u(x,y)exp(-iωt) |
変数分離や複素数に関しては、数学や物理の本を見て下さい。 また、wave equation についても時間があれば勉強しておいて下さい。