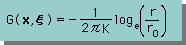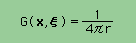
2次元の Laplace equation や Poisson's equation が解決してくれる無限境界の問題は、たくさん有ります。 全部、紹介していると、ハードディスクの容量が足らなくなりますので、ここでは、流体力学の Doublet をベースに話しを進めます。 Doublet とは、sink と source が同一の面に存在する流量 +Q と -Q をもっている流れのことです。Sink とは吸い込みを、source とは吐き出しを意味します。

Doublet は、electromagnetics の勉強で出てくる導線のインダクタンスに深い関係があります。 インダクタンスは、磁束(Φ)と電流(I)との比で決まる値です。 と言うことで、インダクタンスの計算方法についても簡単に紹介します。

■3次元と2次元の違い■
Point charge が3次元の無限空間に存在している場合を考えてみましょう。 無限空間のpoint charge ですから、解は Laplace equation の kernel function になります。下式がそうです。

上式のξは、point charge の位置を示します。xは、point charge の状況を測定する位置です。r は、ξとx間の距離です。

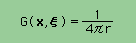
上式を、よーく見ると、無限点では G(x,ξ) がゼロになります。減衰は、1/r になっています(電磁波も1/rで減衰する)。 つまり、無限に大きい3次元の空間は、point charge を吸収できることになります。

2次元の無限空間では、どうでしょう。 解は、下式で表わすことが出来ます。 つまり、2次元のLaplace equation 式の kernel function です。

無限点では G(x,ξ) が、無限大になっています。 2次元では、point charge を吸収できないということを意味しています。