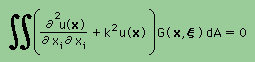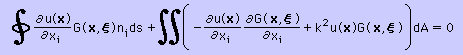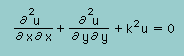
■Helmholtz equation■
上式(U(x,y,t)=u(x,y)exp(-iωt))を wave equation に代入すると下に示すHelmholtz equationが出来上がります。
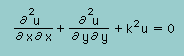
| ▽2u(x,y)+k2u(x,y)=0 |
■Boundary equation■
Laplace equation の時と同様に上の式にWeighted Residual Method を施します。
すると次の様になります。
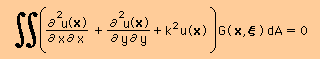
上の式をindex notation で書くと次の様になります。 Index notation についてはFEMのところで勉強しましたがまだ理解していない人はここでもう一度復習しておいて下さいね。