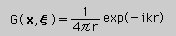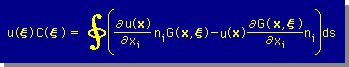Hankel function of the second kind of order zero は、次の複素数で表わされています。

ここに、 J₀をBessel function of the first kind、 N₀を Neumann function of the first kind と言います。そろそろ、頭の中がくしゃくしゃになりそうですね。もーちょっと頑張って下さい。

H₀⁽¹⁾(r) を1回微分すると、負のHankel function of the second kind of order one, H₁⁽¹⁾(r), になります。つまり、下式が成り立ちます。

参考までに、3次元のHelmholtz equation を満足するKernel function は、次の様になります。

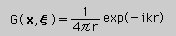3次元のKernel function を計算するのは、いたって簡単ですが、2次元では、Bessel function を計算するサブプログラムをこしらえる必要があります。そのBessel function ですが、計算方法とサブプログラムの作成方法については、後程、詳しく説明します。

■Boundary Equation■
話しを先に進めましょう。Kernel function が見つかれば、Helmholtz equation の境界積分式は、次の様になります。