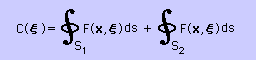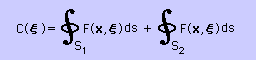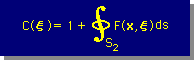前のページの図のξの点について、C(ξ) を計算してみましょう。領域の中には、holeが有りますので、計算式は次の様になります。

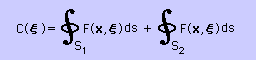無限境界の線上を一周積分すると、結果は1になります。つまり、下式です。理由は、ξの点が領域内にあるからです。

すると、無限領域でのC(ξ) の計算は、下に式で与えられることになります。例えば、ξが領域内にあると、下式の線積分はゼロを生産します。結果的に、C(ξ)=1 になります。ところが、 ξ がhole の中にある場合、線積分は -1 を生産しますので、C(ξ)=0 になります。ここのところは、重要ですので頭に入れておいて下さいね。

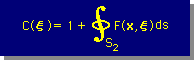
■Bessel Function■
Bessel function は、Bessel の微分方程式を満足する解として、沢山の数学ハンドブックに紹介されています。また、Bessel function の kind とHelmholtz equation との関係も数学の本等に書いてありますので、勉強してください。ここでは、Helmholtz equation に関係している、J₀、J₁、N₀、N₁ のみの計算方法について説明します。

参考にした書物を紹介しておきます。他にも沢山良い本が有りますので、そちらも参考にして下さい。古本でも、十分役立つということですね。

理工学のための数学ハンドブック

数学ハンドブック編集委員会、丸善、1960

常微分方程式とその応用

三木忠夫、コロナ社、1977

BACK	NEXT

Menu

Laplace equation

Helmholtz equation