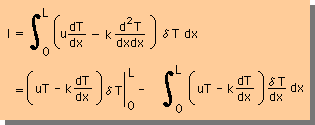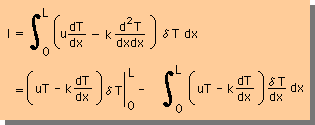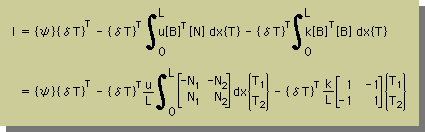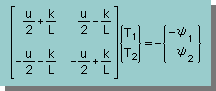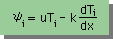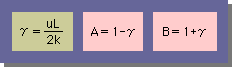よって、上の式が解析しなくてはならない支配方程式だとすると、暗黙的に、 du/dx=0 だと言うことを示唆していることになります。分かりましたか。あまり深く考えると、 一服になりませんので、分からなければ、ここの部分はパスして下さい。

とりあえず、話をすすめることにします。まず、手続きに従って、上の微分方程式の積分式を書きます。 次の様になりますね。

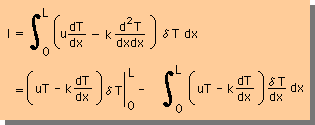さらに、前と同様に、1次要素で上の積分式を近似すると、マトリックス型有限要素式は、 次に様になりますね。

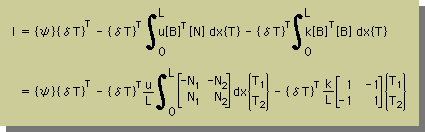そして、∂I/∂{δT} = 0 を計算すると、下に示す有限要素式が出来上がります。 各要素内の u は、要素内の u の平均値を使い、要素内では一定としています。

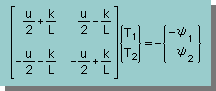	ここに、

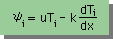どことなく、前に紹介した微分方程式の有限要素式と似ていますね。違う点は、 [N]^T[B]が [B]^T[N]になっています。あれれー、なんか 変だなー、とお思いでしょうが、これで正しいのです。この両者の違いは、 du/dx=0 か又は du/dx≠0 かです。

上の結果を用いて、Global matrix を作り、一般式を取り出すと、前に紹介した 差分式と同じになります。 もちろん、数値計算するときには、u を領域ないで一定にしなくては なりませんがね。

■Difference Equation Analysis■

話をもとに戻しましょう。どこまで戻るかと言うと、あの差分式までです。 そして、差分式をもっと観察し易い様にするために、下のパラメーターを準備しました。

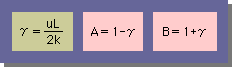ここに、γ＞0 とします。
すると、上の差分式は、次の様に簡略化されます。