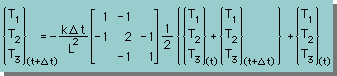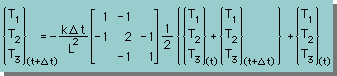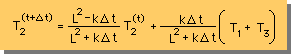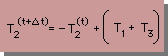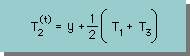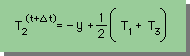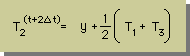■Crank-Nicolson method の安定性■
最後になりましたが、α=1/2 の Crank-Nicolson method の安定性を考えてみましょう。連立方程式は、次の様になります。

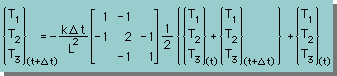これを、T₂について解き、ちょっとアレンジすると、次の様になります。この式は、Explicit method のT₂とImplicit method のT₂の平均になっていることに気付くと思います。そうすると、安定性も2面性を持つことになりそうです。

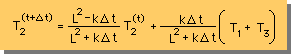この場合も、他の方法と同様に、Δt=0 の場合、 T₂^(t+Δt) = T₂^(t) になります。OKです。では、Δt=∞ の場合はどうでしょう。下式の様になります。

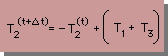見て分かる通り、T₂が無限大になることはないが、なんかちょっと変です。チェックするために、T₂^(t)を下式で与えることにします。つまり、定常解にyを加えた値です。

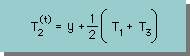上式を、その上の式のT₂^(t)に代入します。すると、結果は、下式の左の様になってしまいます。更に、計算を進めると下式の右の様になります。

この計算を継続しても、T₂は定常解に落ち着くことはありません。つまり、解が下図に示す様に振動していることになります。Crank-Nicolson method は、計算精度が高く、安定しているが、むやみに大きいΔt を使うと、解の信頼性を損ねることになります。

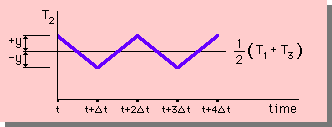この振動を防ぐためには、Δt＜L²/k の条件を維持する必要があります。