■例題1: 波長(λ)=1, 円柱の直径=1■
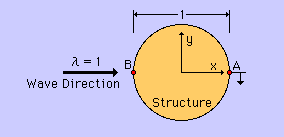
では早速、計算してみましょう。手始めに、厳密解が存在するケースを計算してみます。下図を見て下さい。 波長(λ)が1の波が直径1の円柱にアプローチしている状況を表わしています。波長が1ということは、wave number(k) が2πになることを意味します。

入力データを作成する前に、円柱の境界を要素で分割しておく必要があります。ここでは、上図の点Aから時計方向に、境界を32この線形要素で分割しました。データの作成には、SETLINQ1.FOR で作成しました。すると、BEM1.DAT というファイルが作成されます。要素分割と節点番号の様子を下図に示します。

入力データに誤りが無いと、プログラム HLM8LINQ.FOR は、次の3つのファイルを出力します。

ファイル名	内　　　容
WHCOEFFI.CNT	円柱の境界上の点Aからの円周上の距離と wave coefficientが格納されています。グラフ化は、表計算ソフトで作れます。
SOLUTION.BEM	Helmholtz equationの解析に関する全ての入力/出力データが入っています。
BOUNDARY.BIN	円柱の境界上の{u}と{du/dn}が収められています。バイナリーファイルです。