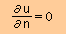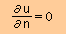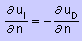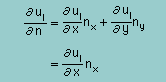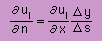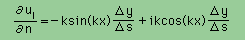■境界条件■
無限点における境界条件は、前に説明した通りです。つまり、無限境界では、何もしないということです。ここでは、構造物の表面の境界条件について説明します。

波は、ソリッド面において、ミラーイメージ的に反射することが知られています。つまり、下式です。

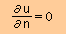そして、u = u_I + u_D ですから、次の条件が成り立ちます。

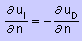u_I(x,y) は、kxの関数ですから、上式の左辺∂u_I/∂n は、次の様になります。∂u_I/∂y は、ゼロであることに注意して下さい。u_Iは、yの関数でないからです。

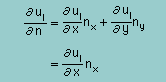仮に、構造物の境界を線形要素で分割すれば、放線ベクトルは、n=(Δyi-Δxj)/Δs となります。Δsは、要素の長さです。Δy=y_i+1-y_i です。すると、上式は、下の様になります。

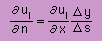上式をスペルアウトすると、下式の様に書けることになります。

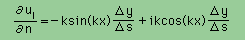これで、境界条件が出来上がりました。ここで紹介している水面波の解析において、境界条件はNeumann型になります。つまり、Dirichlet型がunknown になります。