■勘違い■
実は、文献で紹介されているInterior equation も Bounadry equation も正しい式なのです。しかし、Interior equation から Bounadry equation を導くことに若干(かなり大きい)の勘違いがあったのです。もし、境界要素法の技術者が、C(ξ) の特徴(jump する) を十分に理解していれば、この様な勘違いは、なかったと思います。それ以前に、もし、G. Green が彼の論文で Interior equation は、Bounadry equation にもなると書いておけば、この様な間違いは起こらなかったと思います。

■正しい境界要素法■
これまでは、”勘違い”を説明してきました。では、”正しいBounadry equation の導き方はどうなっているのですか”と言う疑問がわいてきます。答えを言うと、”既に紹介しました”と言うことになります。つまり、境界要素法の積分式(ここでは、境界要素式という) を導く時に、C(ξ) を下式のように、そのままにしておけば良いのです。

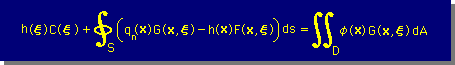
そして、C(ξ) は、ξの位置によって、下式で計算すれば良いのです。

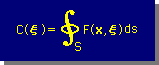
上の2つの式は、ξの位置によって　Interior equation 、 Bounadry equation または、Exterior equation になることが出来ます(もちろん、Exterior equation は、意味の無い式ですが) 。言い替えると、Green 's 2nd Identity にKernal function を挿入して得られた境界要素式の ξ の位置については、なんの制限もありません。多分、G. Green は、たまたま、領域内のC(ξ) が C(ξ)=1 だったので、C(ξ) について説明はしなかったのではないかと、私は思います。

いずれにせよ、Laplace 式の境界要素法では、上の2つの式が、キーになります。ここの部分は、納得して頂けましたか。もし、どうも納得できないという方は、もう一度最初から復習してみて下さい。