これまでの、結果をまとめると：”Laplace equation の場合、F'(x,ξ) は、Source point の近傍で、ゼロまたはある値になる”　という様になります。つまり、下式に示す結果になります。

したがって、C(ξ) は、下式で問題なく計算できます。

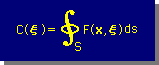
実際に、数値積分を行うと、G(x,ξ)の積分は、Gauss-Legendre の積分点の数の増加にともない、積分精度も上昇します。しかし、F(x,ξ) の積分は、少ない積分点の数で十分な精度が得られます。この事実は、F(x,ξ) がSource point の近傍で well behaved (性格の良い) の関数であることを証明していることになります。

■再度 ベクトルの内積R・nについて■
ベクトルの内積R・n について、追加説明をしておきます。ベクトルの内積R・n を使うと、F(x,ξ)=cos(a)/(2πr) になります。このF(x,ξ) へL'Hospital's rule を適応すると(r goes to 0)、極限は、sin(a)/(2π)(∂a/∂r) になります。角度 a は、r=0の近傍において90度のほぼ定数ですから、∂a/∂r=0になります。結果的に、極限はゼロになります。

■L'Hospital's rule に関する話し■
L'Hospital について簡単に紹介しておきます。
Guillaume Fransois Marquis de L'Hospital (1661-1704) は、フランスのアマチュア数学者で、Johann Berunoulli に数学を学んだことになっています。(Lipman Bers and Frank Karal , CALCULUS, 2nd Ed., Holt Rinehart Winston,1976) 。L'Hospital 's rule は、かなり以前からJohann Berunoulli が発見したことが知られていました。しかし、なぜ L'Hospital 's rule になったかは分かっていませんでした。ところが、最近(多分、私がアメリカ留学中に)になって、Johann Berunoulli からL'Hospital へ宛た手紙がみつかり、文面より L'Hospital が、そのruleをお金で買ったことが判明しました。L'Hospitalが売ってくれと言ったのか、Johann Berunoulliが買わないかと言ったのかは明らかにされていません。