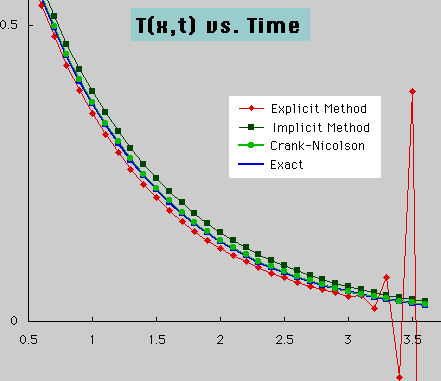
次に、 NSTEP=50 として、α=1, 0, 0.5 で実行すると、下図の様な結果が得られます。

■総合まとめ■
時間項の処理に、3つの方法を紹介しました。Explicit method は、Δtに制限があるが、その代償として、連立方程式を解く必要がありません。つまり、プログラムがシンプルになります。
流体の流れと温度を連立に解く様な複合システムの数値計算では、Explicit methodを使うことは出来ません。
理由は、流れの速度ベクトル(u, v, w)が温度(T)に関係している場合、Explicit methodの様にu,v,w,Tの各々をt=t+Δtで単独に予測する方法は、数値解が発散してしまうからである。
以上のことから、私は個人的にCrank-Nicolson を使います。Implicit method でも差し支えないのですが、同じ労力(連立方程式を解く)をプログラミングに費やすのであれば、精度の良いCrank-Nicolson method を使いましょう、と言うのが理由です。 もし貴方がCrank-Nicolson method を使う場合には、前述の振動に気を付けて下さい。