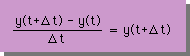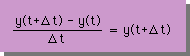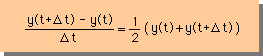■CASE 2 : Implicit Method■
次の方法は、Implicit Method といい、微分方程式の右辺のyを時間t＝t+Δtの値と考えます。つまり、下式です。

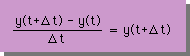この場合、 結果的には、y(t+Δt)・(1-Δt) = y(t) となります。そして、この式を y(t) で割ると次の様になります。

これは、前のExplicit method より一歩前進しているかの様に見えるが、残念ながら Δt² の項の前に(1/2) がmissing しています。つまり、精度的に言って、Explicit method と同じであることになります。

■CASE 3 : Crank-Nicolson Method■
最後に、Crank-Nicolson Method を紹介します。この方法は、微分方程式の右辺のyに時間t＝tの値とt＝t+Δtの値の平均を使っています。式で書くと次の様になります。

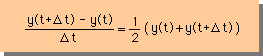この場合、 y(t+Δt)とy(t)の関係式は、y(t+Δt)・(1-(1/2)Δt) = y(t)・(1+(1/2)Δt) となります。そして、この式を y(t) で割ると次の様になります。

これは、前のExplicit method や Implicit method に比べると一歩前進しています。理由は、 Δt² の項の前に(1/2) がきているからです。Δt³ の項の前の定数が(1/6)でなく(1/4) はちょっと残念ですが。しかし、1つ掛け算が増えるだけで精度が上がるのですから、使ってみる価値はあります。