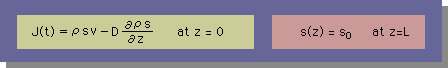
境界条件としては、次に示す様に、上流側がNeumann型で、下流側が、Dirichlet型になっています。
■Program: ONEDEE2.FOR■
早速、上の式を解くプログラムを見てみましょう。上のプログラム名をクリックして下さい。このプログラムにおいて、λの効果は組み込まれていません。これまでに、有限要素法での生成項の取り扱いは、幾度と無く説明してきましたので、λの項は、貴方が組み込んで下さい。
| プログラムでの変数 | 変数の型 | 微分方程式での変数/変数の意味 |
|---|---|---|
| NE | 整数 | 要素数 |
| NNODE | 整数 | 節点数 |
| DT | 実数 | Time step |
| TMAX | 実数 | 時間積分の上限値 |
| IB1, BV1 | 整数、実数 | 上流の境界条件と値 |
| IBN, BVN | 整数、実数 | 下流の境界条件と値 |
| X(I) | 実数 | z |
| RHO(I) | 実数 | ρ(z) |
| V(I) | 実数 | v(z) |
| DB(I) | 実数 | D(z) |
| S(I) | 実数 | s(z) |