の積分式の結果から、u2を計算し厳密解と比較してみよう。だたし、
L1=L2=0.5, α2=1, u1=0, u3=1.0とする。
Integral_by_Element: Problem Page 1
問題 Integral_by_Element -1
の積分式の結果から、u2を計算し厳密解と比較してみよう。だたし、
L1=L2=0.5, α2=1, u1=0, u3=1.0とする。
問題 Integral_by_Element -2
下の2つ積分式を計算すると
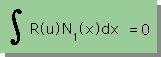 | と |  |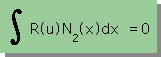
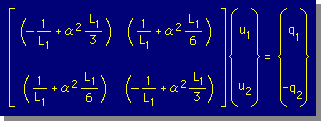
問題 Integral_by_Element -3
領域を3要素で分割し、Helmholtz Equation を数値解析し厳密解と比較してみよう。たたし、
α2=1, L=1, u(0)=0, u(L)=1, L1=L2=0.25, L3=0.5
問題 Integral_by_Element -4
領域を4要素で分割し、Helmholtz Equation を数値解析し厳密解と比較してみよう。たたし、
α2=1, L=1, u(0)=0, u(L)=1, L1-4=0.25, α2=1, u(0)=1, L1-4=0.125とする。
問題 Integral_by_Element -5
Program BUCKLE.FORを用いて、α2=1 のHelmholtz Equation を解きましょう。領域の長さ、境界条件、分割要素数は、下表に示す通りである。なお、領域は等分割するものとする。
| 番号 | 要素数 | At x=0. | At x=L | 領域の長さ | ||
|---|---|---|---|---|---|---|
| 境界条件 | 境界値 | 境界条件 | 境界値 | |||
| 1 | 2 | 1 | 0.0 | 1 | 1.0 | 1.0 |
| 2 | 3 | 1 | 0.0 | 1 | 1.0 | 1.0 |
| 3 | 4 | 1 | 0.0 | 1 | 1.0 | 1.0 |
| 4 | 8 | 1 | 0.0 | 1 | 1.0 | 1.0 |
| 5 | 2 | 1 | 1.0 | 1 | 1.0 | 1.0 |
| 6 | 4 | 1 | 1.0 | 1 | 1.0 | 1.0 |
| 7 | 2 | 1 | 1.0 | 2 | 0.0 | 0.5 |
| 8 | 8 | 1 | 1.0 | 1 | 1.0 | 1.0 |
| 9 | 4 | 1 | 1.0 | 2 | 0.0 | 0.5 |
| 10 | 8 | 1 | 1.0 | 2 | 0.0 | 0.5 |