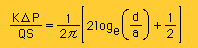変数 u(ξ) を y座標軸上で計算すると、下図の様なグラフが得られます。Charge がpoint でなく分布になっているので、 u(ξ)の peak が無限大になることはありません。

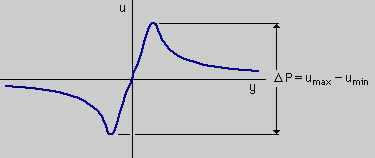上図に示す様に、peak 間をΔPで表わすと、次の関係式が成り立ちます。この式は、q(x) が等分布のときのみに使える近似式です。この式の出所は、後で説明します。

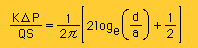ここに、S は、z 軸方向の厚さを意味します。(本当は、Sの代わりにリッターの記号を使いたいのですが、WindowsとMacで表示に違いがあるので使えませんでした)。上の式から言えることは、ΔP/Q は、Qが変化しても、一定の値を示すことになります。

では、実際に計算してみましょう。例えば、q=1/π, a=1, K=1, d=6, S=1 とします。計算を行うために、q(x) が分布している面を要素に分割する必要があります。ここでは、有限要素法で紹介した、4-noded iso-parametric を使うことにします。

q=1/π で a=1 ですから、円の面責はπになり、Q=q×面積ですから、Q=1 になりますね。