■BEM vs. FEM■
境界要素法(BEM)は、有限要素法と同様に微分方程式を解く道具として、構造物の設計に活用されています。しかし、微分方程式を離散化するテクニックには、有限要素法のそれと比較すると、かなり違いがあります。下に違いの幾つかを示します。
| 項目 | 有限要素法(FEM) | 境界要素法(BEM) |
|---|---|---|
| 重み関数 | 有限次数式 | 特異点をもつFundamental solution |
| 部分積分 | 1回使う | 2回使う |
| 積分 | 領域 | 境界 |
| 最小積分領域 | 領域型の要素 | 境界型の要素 |
| 要素分割 | 領域を分割 | 境界を分割 |
重み関数が、微分方程式の a solution であるということは、有限要素法の様に微分方程式の各項毎に離散化が行えないことになります。 つまり、一括処理になります。このことは、プログラミングにも大きな影響を与えています。
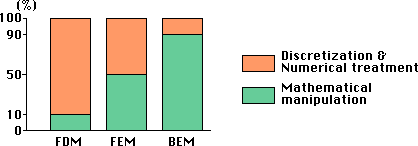
■数学的処理 vs. 数値計算処理■
解析用のソフトを開発するときは、まず微分方程式を離散化が楽に行える段階まで、数学処理を行います。
次は、数値計算法で離散化しフローチャート化します。数学処理が少ないと離散化で苦労することになります。
その代表が差分法です。
また、数学処理が多いと、離散化は楽になりますが、その反面、数学的な拘束が大きくなり、応用範囲が乏しくなります。
その代表が境界要素法です。

最後に、境界要素法ですが、数学的処理の拘束が大きく、応用範囲に制限があるのが現状です。 今日では、様々な技術分野に応用され始めていますが、有限要素法ほどではありません。 しかし、境界要素法には、有限要素法にない様々な素晴しい特徴をもっています。例えば、
■直接法と間接法■
境界要素法には、直接法(Direct method)と間接法(Indirect method) が有ります。
ここでは、直接法で話しを進めていきます。直接法と間接法との違いについては、本文の中で説明します。