Parabolic_Element: Problem Page 1
問題 Parabolic_Element -1
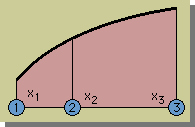
下の図は、2次要素です。
x2=(x1+x3)/2 としたときの、
k12 と k13 を x1からx3まで積分してみよう。
ここに、[kij]=[B]T[B] とする。
さらに、2階微分項の特徴を使ってk11のx1からx3まで積分を求めましょう。この場合、実際の積分計算は必要ありません。
問題 Parabolic_Element -2
下に無次元座標系上の３次要素を示します。
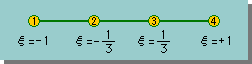
N1(ξ)、N2(ξ)、N3(ξ)、N4(ξ) を求めてみよう。形状関数てしての条件にあっているかどうかもチェックしてみよう。
問題 Parabolic_Element -3
プログラムBUCKLE1A.FORとBUCKLE2A.FORを用いて、次の計算を実行してみよう。Input Dataの作成には、SET1UP.FORを使って下さい。計算を始める前に、全てのEXEファイルを作成しておいて下さい。
計算手順は、(1)SET1UPをキーインする、(2)質問に応えて数値を入力する、(3)BUCKLE1AまたはBUCKLE2Aをキーインする、(4)結果を書き取る、です。
注意：B.C.=1は、Dirichlet型境界条件のことで、B.C.=2はNeumann型境界条件のことです。
| 番号 | 要素 | 要素数 | B.C. at x=0 | B.V. at x=0 | B.C. at x=L | B.V. at x=L | L | 使う Program |
|---|---|---|---|---|---|---|---|---|
| 1 | 1次 | 2 | 1 | 0. | 1 | 1. | 1. | BUCKLE1A |
| 2 | 1次 | 4 | 1 | 0. | 1 | 1. | 1. | BUCKLE1A |
| 3 | 1次 | 6 | 1 | 0. | 1 | 1. | 1. | BUCKLE1A |
| 4 | 2次 | 1 | 1 | 0. | 1 | 1. | 1. | BUCKLE2A |
| 5 | 2次 | 2 | 1 | 0. | 1 | 1. | 1. | BUCKLE2A |
| 6 | 2次 | 3 | 1 | 0. | 1 | 1. | 1. | BUCKLE2A |
| 7 | 1次 | 2 | 1 | 1. | 2 | 0. | 0.5 | BUCKLE1A |
| 8 | 1次 | 4 | 1 | 1. | 2 | 0. | 0.5 | BUCKLE1A |
| 9 | 1次 | 6 | 1 | 1. | 2 | 0. | 0.5 | BUCKLE1A |
| 10 | 2次 | 1 | 1 | 1. | 2 | 0. | 0.5 | BUCKLE2A |
| 11 | 2次 | 2 | 1 | 1. | 2 | 0. | 0.5 | BUCKLE2A |
| 12 | 2次 | 3 | 1 | 1. | 2 | 0. | 0.5 | BUCKLE2A |
計算結果は、u(x) vs. x のグラフにまとめましょう。また、解析の収束の度合をみるために、x=0.5 での誤差と節点数もグラフにしてみよう。ここで、誤差とは厳密解マイナス数値解析解の絶対値を意味します。